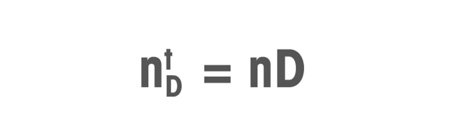Refractive Index: All You Need to Know

The refractive index n of a medium (e.g., water, olive oil, etc.), also called the index of refraction, is defined as the quotient of the speed of light in vacuum c and the speed of light in the medium v. It is a dimensionless number that depends on the temperature of the medium and the wavelength of the light beam.  

In simple words, the index of refraction describes how fast a light beam travels through a medium compared to a vacuum. This relationship is described by the formula:

n = c / v

On this page, you will gain essential knowledge about refractive index and refractive index measurements.

Learn more about the definition of refractive index, applications, how to measure it, and much more.  

Just download our refractometry guide PDF to learn more about refractive index measurement.

This free guide will help you learn more about refractometry, including how to avoid errors when measuring refractive index.

Index of refraction and refractive index are different names for the same thing, as noted above. Which term is used depends largely on where you live. For example, people in the U.S. often use "index of refraction" whereas people in India tend to use "refractive index". We will use these terms interchangeably in this discussion.

Refractometry is an analytical method used to measure the refractive index of a sample to determine its composition or purity. Refractometry is a qualitative and non-destructive technique that is based on Snell's law.

The refractometry method, which is largely used in industry for quality control purposes, uses a  refractometer. We will discuss refractometry and use of refractometers in the chapters that follow.

Before we dive into the technical explanation of refractive index, let's look at a visual example that shows the speed of light and the refractive index effect in different media.

Here, glass rods are immersed in three glasses filled with different media:

Glass Media
1. Water
2. Water and cedar oil
3. Cedar oil

What is happening in each glass?

Water has a lower refractive index (n = 1.333) than the glass rod (n = 1.517). Therefore, it is possible to see the entire rod in glass 1 and part of the rod in glass 2.

On the other hand, the glass rod (n = 1.517) and the cedar oil (n = 1.516) have almost identical refractive indices. This causes the immersed rod to seem to disappear in the cedar oil (partially in glass 2 and fully in glass 3).

Based on Snell's law refractometers were developed to measure the refractive index of liquids and semi-solid samples.

A digital refractometer measuring cell has a schematic setup based on Snell's law. Therefore, it relies on total internal reflection and the critical angle. Here is how it works:

The light source (1) is a light-emitting diode (LED). The emitted LED beam passes through a polarization filter (2), an interference filter (3), and a focal lenses (4) before it reaches the sample via the sapphire prism (5).

The reflected light (angle of incidence > critical angle) is deflected via a lens (6) to the optical sensor CCD (7) that determines the critical angle. In addition, modern digital refractometers automatically control the temperature in the prism/sample boundary to enhance the accuracy of the measurement.

A digital refractometer measures the refractive index or related values of a liquid sample using the total reflection method. This measurement is done automatically, which reduces operator influence and enhances accuracy. Using a small sample volume (0.5 to 1 mL), highly accurate measurements of the index of refraction are performed in seconds.

Manual refractometers such as Abbe refractometers can also be used to measure refractive index. However, they are being replaced rapidly by digital, often handheld refractometers.

So what is the relationship between refractive index determination and temperature?

First, we need to understand the effect of temperature on a liquid sample. Temperature influences the space in which atoms fit together to create a molecule. Atomic vibration increases as temperature increases, which causes the atoms to move farther apart and reduces the optical density value of the sample medium.

As noted previously, the refractive index describes how fast a light beam travels through media. If a medium is less optically dense due to a temperature increase, the light will travel faster, which causes the deflected angle to shift slightly. In other words, the higher the temperature, the lower the refractive index, as shown in the graph below which uses water as the sample medium.

As you can see, the sample temperature has a major influence on the measurement procedure. Therefore, temperature must be accurately measured and, if possible, controlled.

Older instruments such as Abbe refractometers may require a water bath to control the temperature, while many modern, digital refractometers use Peltier elements to control the system temperature. This ensures a fast and accurate determination of the refractive index value.

In a refractive index measurement, the wavelength of the light beam matters because of the effect of dispersion on the properties of waves in a medium (known as dispersion relation). Almost all substances have different refractive indices that also differ depending on the wavelength used. This dispersion relation can be calculated as follows.

We know that the speed of light in a medium is:

v = c/n

Where:
n is the index of refraction
c is the speed of light in a vacuum (or air)
v is the speed of light in the media

Similarly, the wavelength in the same medium is:

λ = λ₀/n

where λ₀ is the wavelength of that light in a vacuum (or air).

Therefore, the refractive index (n) is inversely proportional to the wavelength and also to the speed of light. This means the greater the wavelength, the lower the refractive index. This relationship is represented by the equation:

v(λ) = c/n(λ)

However, for industrial applications where refractive index measurement is required, it is necessary to have a defined, precise wavelength to allow the refractive index measurement of different samples to be analyzed under the same conditions for quality control.

To generate a defined wavelength, refractometers most often use the sodium D-line, which corresponds to 589.3 nm. Due to the fact that it is a widely available, reliable and stable light source, the sodium D-line has long been used in the study of refractive index.

n = the refractive index

t = temperature (°C)

D = the D-line of sodium

However, the refractive index is generally represented more simply as nD.

Refractive index measurement checks the purity and concentration of liquid, semi-liquid and solid samples. Refractive index values can also be determined for gases. When using a digital refractometer, liquids and semi-liquid samples can be measured with high accuracy (e.g. down to - / + 0.00002). Gas and solid samples require specialized instruments or accessories for accurate refractive index measurement.

In addition, the index of refraction can be correlated to a wide range of concentrations which can be used to characterize many different samples in many different industries and applications, such as:

• Food and beverage: Measuring the Brix (sugar content) of soft drinks or the Oechsle of grape must used in winemaking.
• Chemical: Determining freezing point (⁰C or ⁰F), acid/base concentration, or the presence of organic solvent and inorganic salt in % w/w or v/v.
• Pharma: Measuring hydrogen peroxide or methanol percentages, or assessing concentrations of various substances in human urine.

Additionally, for some applications, combining refractive index with a density measurement creates a simple yet powerful quality control technique. These determinations can be fully automated.

Besides the Brix scale there are other comparable scales for indicating sucrose content in a sample, such as degrees Plato, Baumé, Oechsle and Balling. Learn more about their differences, calculations, usage and how to measure.

Absolute refractive index is calculated with reference to the vacuum in which light propagates with the greatest possible speed of 299,792,458 meters per second (the speed of light). However, in practice, the air we breathe is also considered a reference medium, even though light propagates at a slightly slower speed (1.0003 times slower) than it does through a vacuum.

Thus, we can say that the absolute refractive index measures how many times the speed of light is greater in a vacuum (or air) than in any other media.

Here is a practical example of the absolute refractive index of water at 20 °C, through which we know light travels at 2.25 x 10⁸m/s.

This means that light travels 1.33333 times slower through water than through a vacuum (or air).

Relative refractive index is defined as the ratio of the light velocities between any two media other than a vaccum (or air). For example, one could measure the refractive index of olive oil relative to the refractive index of water. However, there is no practical use for measuring relative refractive index in industrial applications.

Modern digital instruments can easily determine the refractive index of liquids with a high degree of accuracy. However, high-resolution instruments are no guarantee of accurate results. Good measurement principles must also be applied.

For example, did you know that insufficient cleaning of the prism—or simply wiping off old sample with a cloth—can drastically falsify your next measurement?

Because these instruments measure the angle of total reflection off the surface of the prism, even the thinnest layer of old sample will have a significant impact on the refractive index measurement of any new sample added to it.

Download the Refractive Index Measurement Guide and learn helpful tips and hints to avoid errors when measuring the refractive index of liquids.

Whether you work with chemicals, foods, beverages, or other products that can be pasty or liquid, there are important details that need to be addressed in order to improve your refractive index analyses. These include questions such as:

• How often should I calibrate my instrument?
• Which solvent should I use to clean the measuring cell / prism?
• My sample is pasty / viscous. What is the best way to handle and measure it?

The answers to these questions can directly influence your determinations. Check out our interactive booklet that answers the most-asked questions about refractive index, Brix and density measurements!